Como abrir autos de diferente marca con un alambre
Una ecuación de segundo grado con una incógnita es una igualdad o expresión algebraica que se puede expresar de la forma ax2+bx+c=0, siendo a, b y c números reales y a distinto de 0.
Como son las ecuaciones de segundo grado
La expresión general de un ecuación de segundo grado es.ax2+bx+c=0
ax2+bx+c=0 es un polinomio de segundo grado igualado a 0.
Para resolver una ecuación de segundo grado es conveniente expresarla primero en forma general, pasando todos los términos al miembro de la izquierda y reduciendo después los términos algebraicos semejantes.
Como expresar las ecuaciones de segundo grado antes de resolverlas
Ecuación expresión términos3x2+2x=5 3x2+2x-5=0 a=3, b=2, c=-5
5x2=-4x 5x2+4x=0 a=5, b=4, c=0
3x(x+2)=0 3x2+6x=0 a=3, b=6, c=0
Como resolver ecuaciones de segundo grado completas
Una ecuación de segundo grado es completa cuando todos sus coeficientes son distintos de cero, es decir, si b y c son distintos de cero.Formula para resolver ecuaciones de segundo grado
Para obtener las soluciones de una ecuación de segundo grado utilizamos la siguiente fórmula.el doble signo ± indica que pueden existir dos soluciones.
Ejemplos
Encontramos las soluciones de las siguientes ecuaciones.
En la ecuación x2+5x+6=0
Aplicando la fórmula para resolver este tipo de ecuaciones, siendo a=1, b=5 y c=6 (que corresponden a los coeficientes de los términos de la ecuación) tenemos.
(-2)2+5*(-2)+6=0
(-3)2+5*(-3)+6=0
Resolvemos la ecuación 2x2-5x+2=0
Aplicando la formula para resolver ecuaciones de segundo grado tenemos.
Ecuaci0nes de segundo grado con fracciones y parentesís
Para resolver ecuaciones de segundo grado con fracciones y parentesis seguimos los siguientes pasos.1- Eliminamos los denominadores (ecuaciones con fracciones)
2- eliminamos parentesís, ya que es como resolver ecuaciones de primer grado
3- Pasamos todo al primer miembro, igualamos a cero para obtener una ecuación de segundo grado ordenada.
4- Reducimos términos semejantes y si es posible simplificamos.
5- Resolvemos la ecuación con la formula para resolver ecuaciones de segundo grado.
6- Comprobamos sustituyendo x en la ecuación original.
Resolvemos la siguiente ecuación de segundo grado con fracciones y parentesis
1- Eliminamos las fracciones. calculamos el m.c.m de los denominadores y multiplicamos los miembros de la ecuación por el.
El m.c.m de (2,4)=4,
Eliminando los denominadores tenemos.
2(x-1)2-(3-4x)=(5+4x)
2- En este caso podemos observar que en el término de segundo grado 2(x-1)2 tenemos el cuadrado de una diferencia dentro del parentesis, usamos las igualdades notables para eliminar este cuadrado de una diferencia. nos queda. 2(x2-2x+1)-(3-4x)=(5+4x)
Eliminando los parentesis.
2x2-4x+2-3+4x=5+4x
Pasando todo al primer miembro, igualando a cero.
2x2-4x+2-3+4x=-5-4x=0
Eliminando términos semejantes.
2x2-4x-6=0
Eta ecuación la podemos simplificar dividiendo por 2 para obtener una ecuación mas sencilla.
x2-2x-3=0
Resolvemos la ecuación de segundo grado obtenida utilizando la formula para resolverlas.
Las soluciones de esta ecuación son 3,-1
Podemos comprobar sustituyendo en la ecuación original y comprobando que se cumple la igualdad algebraica.
Soluciones de una ecuación de segundo grado
Observamos que en la formula para resolver ecuaciones de segundo grado completas, encontramos la expresión.Esta raiz cuadrada solo existirá cuando el radicando sea positivo o 0.
El radicando b2-4ac se llama discriminante y se suele simbolizar con un triangulo pequeño ∆. El número de soluciones de una ecuación de segundo grado (llamadas también raíces) depende del signo del discriminante y se puede saber antes de resolver la ecuación.
∆=b2-4ac>0
La ecuación tiene dos soluciones distintas.
∆=b2-4ac=0
La ecuación solo tiene una solución doble o raiz doble.
∆=b2-4ac es menor a 0
La ecuación no tiene ninguna solución ya que no existe raíz cuadrada negativa.
Estudiamos el número de soluciones de la ecuación 2x2+5x+6=0 sin resolverla (verificando el discriminante)
El valor del discriminante es -23
La ecuación no tiene ninguna solución real.
calculamos el número de soluciones de la ecuación 2x2-20x+50=0
Calculando el discriminante observamos que es 0.
La ecuación tiene una única solución.





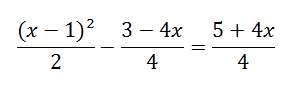





alguien que me ayude con esta ecuacion de segundo grado
ResponderEliminar3(x+2)(x+3)=60
Por favor necesito ayuda con este ejercicio de ecuacion de segundo grado(y-2) (y-3) = 9y+ 6
ResponderEliminarCual seria el resultado dex/2=7
ResponderEliminar???? Ayúdenme por favor
El 2 está dividiendo a la x, por lo que "pasa" multiplicando:
Eliminarx = 7 * 2
x = 14