En el polinomio con ese divisor, P(x)=(x-a)*C(x)+R(x) el grado del cociente C(x) tiene que ser una unidad inferior al grado del dividendo.
Como usar la regla de Ruffini y que pasos seguir
Calculamos la siguiente división.(x3+1)/(x-2)
1-Escribimos todos los coeficientes de todos los monomios del dividendo de mayor a menor grado(como si estuviera completo y ordenado, tomando los coeficientes que no aparecen como valor 0).
En este caso el dividendo.
x3+1
completo, ordenado y con sus coeficientes.
=1x3+0x2+0x+1 Los coeficientes son 1 0 0 1
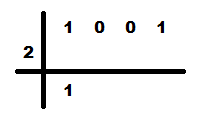
2- Tomamos el término independiente del divisor cambiado de signo y lo colocamos a la izquierda, podemos ordenar la operación de la siguiente manera.
3- Bajamos el primer coeficiente en la fila de resultados.
4- Multiplicamos el termino independiente por el coeficiente que bajamos, el resultado lo sumamos al siguiente coeficiente y bajamos.
En este caso multiplicamos 2*1, sumamos el siguiente coeficiente que es 0 y bajamos el resultado.
5- Repetimos el proceso hasta que se terminen los coeficientes.
El ultimo número de la operación es el resto de la división, los tres primeros números son los coeficientes del resultado de la división original (ponemos el grado del resultado un grado menor que el dividendo original, si en el resultado hay coeficientes de grado 0, no se anotan en el).
En el ejemplo seria.
Vemos que los coeficientes del resultado son.
1,2,4 C(x)=x2+2x+4
Podemos comprobar que.
x3+1=(x-2)*(x2+2x+4)+9
Para utilizar la regla de Ruffini es necesario que P(x) esté expresado de forma completa, es decir, si es de grado n, debe contener todos los términos de grado menor o igual que n. Si P(x) no es completo, como, por ejemplo: P(x)=x3-3, lo consideramos de forma: P(x)=x3+0x2+0x-3.Donde los coeficientes son 1 0 0 -3
Realizamos la siguiente división usando la regla de Ruffini.
(x4+2x3-3x2-6)/(x+2)
Considerando completo el dividendo, los coeficientes son 1 2 -3 0 -6
El termino independiente del divisor cambiado de signo es -2
Usando la regla de Ruffini realizamos la operación.
Realizando la operación obtenemos los siguientes coeficientes y resto.
Observamos que no anotamos el termino de segundo grado en el resultado ya que el coeficiente es 0, por lo tanto es nulo el valor.
Divisores de la forma (-x-b) o (-x+b) en la regla de Ruffini
La regla de Ruffini solo se puede aplicar a divisores del tipo (x-a) o (x+a), es decir, para polinomios de grado 1, donde el coeficiente de x sea 1.Cuando el divisor es del tipo (-x-a) o (-x+a)
Ejemplo
(x3+2x2-3x-6)/(-x+2)
Para poder usar la regla de Ruffini es necesario que el divisor sea del tipo (x+a) o (x-a) por lo que para poder usarla en el ejemplo anterior cambiamos de signo todos los términos de los dos miembros.
Cambiando los signos en el ejemplo, nos queda la siguiente operación.
(-x3-2x2+3x+6)/(x-2)
Ahora que tenemos un divisor del tipo (x-a) aplicamos la regla de Ruffini.
Los coeficientes son -1 -2 3 6
El termino independiente del divisor cambiado de signo es 2 (que es lo mismo que +2)
Operando obtenemos el resultado y resto.
Divisores de la forma ax-b en la regla de Ruffini
Para utilizar la regla de Ruffini en una división en la que el divisor es de la forma (ax-b) procedemos de la siguiente manera.Ejemplo
Realizamos la siguiente división.
(x2+2x-3)/(2x-6)
1- Dividimos el divisor entre a, es decir, entre el coeficiente de x en el divisor.
(2x-6)/2=(x-3)
Como vemos hemos obtenido un nuevo divisor de la forma (x-a) ahora podemos aplicar la regla de Ruffini.
Los coeficientes de dividendo son 1 2 -3
El termino independiente del nuevo divisor cambiado de signo es 3
Operando tenemos.
El resultado o cociente de la división original sera el cociente de esta división dividido por el número que dividimos el divisor inicial, es decir, en este ejemplo, dividido entre 2
Cociente o resultado de la división original.
El resto no varía, es decir, en la división original el resto es 12.





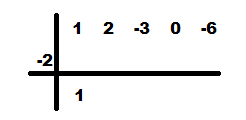




No hay comentarios:
Publicar un comentario