Las fracciones algebraicas se comportan, en muchos casos, como las fracciones numéricas y se trabaja con ellas utilizando la mismas técnicas.
Ejemplos de fracciones algebraicas
Son fracciones algebraicas.Fracciones equivalentes
Dos fracciones algebraicas son equivalentes cuando se cumple la igualdad.Verificamos si las siguientes fracciones algebraicas son equivalentes.
Estas dos fracciones son equivalentes, porque se cumple la igualdad.
(x2-2x-3)(x+2)=(x3-7x-6)
(x2-x-6)(x+1)=(x3-7x-6)
Simplificación de fracciones algebraicas
Simplificar una fracción algebraica es encontrar otra fracción equivalente a ella sin factores comunes en el numerado y el denominadorpara simplificar una fracción algebraica, primero usamos la factorización de polinomios en el numerado y el denominador y eliminamos todos los factores comunes que sea posible.
Cuando los términos de una fracción algebraica no se pueden dividir por un mismo número entero o polinomio, Cuando obtenemos una fracción equivalente a la original, decimos que es irreducible.
Las siguientes fracciones algebraicas son irreducibles.
Simplificamos la siguiente fracción algebraica.
En este ejemplo se puede factorizar el denominador.
x3-x2-x+1=(x-1)2(x+1)
Sustituimos el resultado en la fracción original, factorizando lo más posible.
Ahora reducimos los términos semejantes realizando las divisiones del numerador entre el denominador, es decir, si existen los mismos monomios, los eliminamos por pares del numerador y el denominador.
En este caso tenemos (x-1) en el numerador y en el denominador, realizamos la división, es decir, (x-1)/(x-1)=1, el resultado lo anotamos en el numerador y nos queda.
Esta es una fracción equivalente a la inicial, también podemos aplicar las igualdades notables (suma por diferencia) para expresar la fracción sin factores, es decir.
Simplificamos la fracción.
1- Factorizamos numerador y denominador.
numerador x2+x = x(x+1)
denominador x2+2x+1 = (x+1)2=(x+1)(x+1)
2- Sustituimos en la fracción original.
3- Eliminamos los términos semejantes (dividimos los términos semejantes y el resultado lo anotamos en el numerador).
hemos simplificado la fracción original (encontrando una fracción equivalente a la inicial).
Reducir a común denominador
Reducir a común denominador dos fracciones algebraicas es encontrar otras fracciones equivalentes que tengan igual el denominador1- Multiplicamos todos los denominadores de las fracciones, el resultado es el nuevo denominador común de todas ellas.
2- Dividimos el nuevo denominador común entre el denominador de cada fracción original y el resultado se multiplica por el numerador.
3- Mantenemos el denominador común en cada fracción.
Reducimos a común denominador las siguientes fracciones algebraicas
El denominador común es.
(x)*(y2)*(xy)=x2y3
Continuamos con el segundo paso (dividir el denominador común entre cada denominador y el resultado multiplicarlo por el numerador).







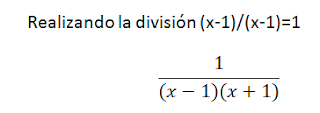






estupendo resumen :) me a servidoo muxoo
ResponderEliminarEs 1/4(3x-5/4) = 3/4(25/8-x) - 55/32 como resolverla ayuda
ResponderEliminarcomo se resuelven las ecuaciones con fracciones algebraicas no entiendo ayuda
ResponderEliminarcomo se resulven las ecuaciones fraccionarias con incognitas por ejemplo 1/2 z = -5
ResponderEliminarNo me sirvio por q necesitaba el ejercio hecho de una vez no paso por paso. Peroen los resumenes muy bn me ayudaron vastantes...........
ResponderEliminarDe malas por sincera mente esta respuesta esta muy bn formulada y los resumenes estan muy bn lo siento pero si no te gusto demalas listo..........
EliminarAndreina dh osorio yo a vos te quiero y vastante N.L.O te amooooo mor yo con vos hasta el final ojala se cumpla este sueÑo ;) tqm........
ResponderEliminar